[CS231n] 3. Loss Functions and Optimization

어떤 W가 가장 좋은지 -> 지금 만든 W가 좋은지 나쁜지를 정량화 할 방법 필요

- W를 입력으로 받아 각 스코어를 확인하고, 이 W가 지금 얼마나 bad 한지 정량적으로 말해주는 것: Loss Function

- 행렬 W가 될 수 있는 모든 경우의 수 중 가장 덜 bad 한 W가 무엇인지 : Optimization

 

* 정답 score가 다른 score보다 높으면 좋다 !!!

 

 

Multi-class SVM loss

: 여러 클래스를 다루기 위한 이진 SVM의 일반화된 형태

- 손실함수 L_i을 구하기 위해선 우선 'true인 카테고리'를 제외한 '나머지 카테고리 Y'의 합을 구한다.

 (즉, 맞지 않은 카테고리 전부를 합침)

- and 올바른 카테고리의 score과 올바르지 않은 카테고리의 score을 비교한다.

- If 올바른 카테고리 score > 올바르지 않은 카테고리 score

   - 일정 safety margin 이상이라면 (ex. 1)

   - then, true score가 다른 false 카테고리보다 훨씬 크다는 뜻

   - Loss = 0, 이미지 내 정답이 아닌 카테고리의 모든 값을 합치면 이 이미지의 최종 Loss가 되는 것

   - then, 전체 training data set에서 그 loss들의 평균을 구함

 

 If true class의 score가 제일 높으면:
 	then, max(0, s_j - s_yi + 1)

 

 

 

hinge loss

- 0과 다른 값의 최댓값, Max(0, value)와 같은 식으로 손실함수를 만듬

(출처: Standford University CS231n, Spring 2017)

정답 카테고리의 점수가 높아질수록 Loss가 선형적으로 줄어든다.

- 이 Loss는 0이 된 이후에도 Safety margin을 넘어설 때까지 더 줄어든다.

  (Loss=0; 클래스를 잘 분류했다.)

 

* s: 분류기의 output으로 나온 예측된 score

ex) 1(고양이), 2(개)

   -> S_1(고양이 score), S_2(개 score)

* y_i: 이미지의 실제 정답 category (정수 값)

* s_y_i: training 셋의 i번 째 이미지의 정답 class의 score

 

 

 

 

(1) Cat이 정답 class 일 경우

(출처: Standford University CS231n, Spring 2017)

Cat의 Loss = 5.1 - 3.2 + 1(margin)

                   = 2.9 : Loss가 발생했다!

Car의 Loss = 3.2

Frog의 Loss = -1.7

 

=> Cat의 score는 Frog의 score보다 훨씬 크므로 Loss는 0이라고 할 수 있다.

 

 

고양이 image의 Multiclass-SVM Loss는 이런 클래스 쌍의 Loss의 합이 되며, 즉 2.9 + 0 = 2.9

(출처: Standford University CS231n, Spring 2017)

- 여기서 2.9라는 숫자는 '얼마나 분류기가 이 이미지를 bad하게 분류하는지' 에 대한 척도가 될 것

 

 

 

(2) Car이 정답 class 일 경우

(출처: Standford University CS231n, Spring 2017)

- Car & Cat -> Loss=0

- Car & Frog -> Loss=0

 

(출처: Standford University CS231n, Spring 2017)

 

 

 

(3) Frog이 정답 class 일 경우

(출처: Standford University CS231n, Spring 2017)

(출처: Standford University CS231n, Spring 2017)

 

 

 

(4) 최종 Loss

(출처: Standford University CS231n, Spring 2017)

- 전체 training set의 최종 Loss는 각 training image의 Loss들의 평균

: (2.9 + 0 + 5.27) / 3

- 우리의 분류기가 5.3점만큼 이 training set을 bad하게 분류하고 있다는 '정량적 지표' !

 

 

 

Q. margin은 어떻게 정하는 것인가?

- 우리는 실제 loss function의 score가 정확히 몇인지를 신경쓰는 것은 아니다.

- 중요한 것은 여러 score간의 상대적인 차이 !

- 정답 score가 다른 score에 비해 얼마나 더 큰 score을 가지고 있느냐! 가 중요

 

 

 

Q1. What happens to loss if car scores change a bit?

A. Car의 score를 조금 바꾸더라도 Loss가 바뀌지 않을 것이다.

  - SVM loss는 오직 정답 score과 그 이외의 score만 고려했다.

  - Car의 score가 이미 다른 score들보다 엄청 높기 때문에 결국 Loss는 변하지 않고 0일 것이다.

 

Q2. What is the min/max possible loss?

A. min = 0

    max = infinity  (hinge loss를 봐도 알 수 있음)

 

Q3. At initialization W is small so all s=0, what is the loss?

- 파라미터를 초기화하고 처음부터 학습시길 때 보통 W를 임의의 작은 수로 초기화시키는데, 

- 이렇게 되면 처음 학습 시 결과 score가 임의의 일정 값을 갖게 된다.

A. number of classes - 1

- Loss를 계산할 때 정답이 아닌 class들을 순회한다. = C-1 class들을 순회함

- 비교하는 두 score가 거의 비슷하니 margin 때문에 1 score를 얻게 될 것

- Loss = C-1

 

Q4. What if the sum was over all classes? (including j=y_i)

(SVM은 정답인 class 빼고 다 더한 것인데, 정답인 class도 더하면 어떻게 될까?)

A. Loss에 1이 더 증가할 것

 

Q5. What if we used mean instead of sum?

A. 영향을 안 미친다. (scale만 변할 뿐)

 

Q6. What if we used

A. 결과는 달라질 것

- 실제로도 squared hinge loss를 사용함

 

 

 

 

Multiple SVM Loss: Example code

def L_i_vectorized(x, y, W):
    scores = W.dot(x)
    margins = np.maximum(0, scores-scores[y] + 1)
    margins[y] = 0 # max로 나온 결과에서 정답 class만 0으로 만들어줌
    		# 굳이 전체를 순회할 필요 없게 해주는 일종의 vectorized 기법
    loss_i = np.sum(margins)
    return loss_i

- numpy를 이용하면 loss function을 코딩할 수 있다. (easy)

- max로 나온 결과에서 정답 class만 

 

 

E.g. Suppose that we found a W s.t L=0. Is that W unique?

A. 다른 W도 존재한다. ex. 2W is also has L=0.

-> margin도 2배일 것

 

(출처: Standford University CS231n, Spring 2017)

 

 

우리는 오직 data의 loss에만 신경을 쓰고 있고, 분류기에게 training data에 꼭 맞는 W를 찾으라고 말하는 것과 같다.

-> 실제 우리는 training data에 얼마나 꼭 맞는지는 전혀 신경쓰지 x

-> training data를 이용해 어떤 분류기를 찾고, 이를 test data에 적용할 것

-> test data에서의 성능이 중요하다.

-> training data에서의 Loss만 신경쓴다면 좋지 x

 

 

 

Regularization

(출처: Standford University CS231n, Spring 2017)

- 모델이 좀 더 단순한 W을 찾도록 함

- Loss Function은 Data Loss와 Regularization의 두 가지 항을 가진다.

   - 람다: 하이퍼 파라미터; 실제 모델 훈련할 때 고려해야 할 중요한 요소

 

종류

(출처: Standford University CS231n, Spring 2017)

 

- Regularization은 모델이 training data set에 완벽히 fit하지 못하도록 모델의 복잡도에 penalty를 부여하는 방법

(overfitting을 방지하는 것이라고 알고 있음)

 

 

 

 

Softmax

(출처: Standford University CS231n, Spring 2017)

 - score을 전부 사용하는데, score들에 지수를 취해 양수가 되게 만든다.

- 그 짓들의 합으로 다시 정규화 시킴

=> softmax 함수를 거치게 되면 확률 분포를 얻을 수 있음

   (해당 클래스일 확률)

 

(출처: Standford University CS231n, Spring 2017)

- softmax에서 나온 확률이 정답 class에 해당하는 확률을 1로 나타나게 하는 것

- 우리가 원하는 것) 정답 class에 해당하는 class의 확률이 1에 가깝게 계산되는 것

   - Loss는 '-log(정답class확률)' 이 될 것

   - Loss function은 '얼마나 좋은지'가 아니라 '얼마나 bad한지'를 측정하는 것이기 때문에 마이너스(-)를 붙인다.

 

 

(출처: Standford University CS231n, Spring 2017)

- score가 있으면 softmax를 거치고, 나온 확률 값에 -log를 추가해주면 된다.

 

 

 

 

고양이 예제로 돌아간다면, (linear classifier의 output으로 나온 / SVM Loss의 결과) score 자체를 쓰는 것이 아니라 지수화 시켜 쓰자.

-> 합이 1이 되도록 정규화 시켜 주기

-> 정답 score에만 -log를 취해주기 : "softmax" / "multinomial logistic regression"

(출처: Standford University CS231n, Spring 2017)

 

Q. What is the min/max possible loss L_i?

A. min = 0, max = infinity

 

- 우리는 정답 class의 확률은 1이 되기를, 정답이 아닌 class의 확률은 0이 되길 원한다.

- 즉, log 안의 어떤 값은 1이 되어야 한다. => -log(1) = 0

   - 고양이를 완벽하게 분류했다면 Loss=0 일 것

 

Q. Loss=0이라면 실제 score은 어떻게 되어야 할까?

A. score는 infinity에 가까워야 할 것이다.

 

- 만약 정답 class의 확률이 0 => -log(0) : + infinity (불가능, 지수=0이 될 수 없다.)

- '유한 정밀도'를 가지고 최댓값(무한대), 최솟값(0)에 도달할 수 없다.

 

 

*

최종 Loss Function이 최소가 되게 하는 가중치 행렬이자 파라미터인 행렬 W를 구하게 되는 것

-> 어떻게 Loss를 줄이는 W를 찾는 것 ??

-> "최적화(Optimization)"

 

 

Optimization

(1) A first very bad idea solution: Random search (임의 탐색)

# assume X_train is the data where each column is an example (e.g. 3073 x 50,000)
# assume Y_train are teh labels (e.g. 1D array of 50,000)
# assume the function L evaluates the loss function

bestloss = float("inf") # Python assigns the highest possible float value
for num in xrange(1000):
    W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
    loss = L(X_train, Y_train, W)
    if loss < bestloss: # keep track of the best solution
        bestloss = loss
        bestW = W
    print ('in attempt %d the loss was %f, best %f' %(num, loss, bestloss))

- 임의로 샘플링한 W들을 엄청 많이 모아두고 Loss를 계산하여 어떤 W가 좋은지 살펴보는 것

 

Let's see how well this works on the test set ...

# Assume X_test is [3073 x 10000], Y_test [10000 x 1]
scores = Wbest.dot(Xte_cols) # 10 x 10000, the class scores for all test examples

# find the index with max score in each column (the predicted class)
Yte_predict = np.argmax(scores, axis=0)

# and calculate accuracy (fraction of predictions that are correct)
np.ean(Yte_prdict == Yte)

# returns 0.1555

- CIFAR-10에서 class는 10개이므로 임의 확률은 10%가 되고,

  random search를 거치게 되면  15%의 정확도를 보임

 

 

(2) Follow the slope: Local gemetry

- NN, Linear Classifier을 훈련시킬 때 일반적으로 사용하는 방법

 

* 경사(slope): 1차원 공간에서는 어떤 함수에 대한 미분값

= 도함수(derivative)

(출처: Standford University CS231n, Spring 2017)

-> 다변수 함수에서도 확장 가능

- 다변수에서 미분으로 일반화 시킨 것이 gradient

 

gradient의 방향: 함수에서 '가장 많이 올라가는 방향'

 

 

 

크고 복잡한 알고리즘 학습시키는 방법

Gradient Descent

while True:
    weights_grad = evaluate_gradient(loss_func, data, weights)
    weights += - step_size * weights_grad # perform parameter update

- 우선 W를 임의이 값으로 초기화시킴

- then, Loss와 gradient를 계산한 뒤 가중치를 gradient의 반대 방향으로 update

   - gradient가 함수에서 증가하는 방향이기 때문에 -gradient를 해야 내려가는 방향이 됨

   - 반복하다보면 결국 수렴할 것

- step size는 하이퍼 파라미터; gradient 방향으로 얼마나 나아가야 하는지를 알려줌

   - learning rate라고도 하며, 매우 중요 !

 

 

Stochastic Gradient Descent (SGD)

- Loss Function에서 우리는 전체 training set들의 loss의 평균을 구했다.

- but, 실제로 N이 엄청나게 커질 수 있다.

(출처: Standford University CS231n, Spring 2017)

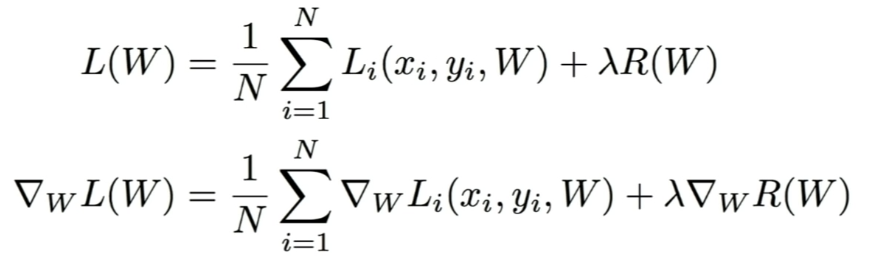
-> Loss를 계산하는 것이 굉장히 오래 걸리는 작업이 됨 (수백만 번의 계산)

# vanilla minibath gradient descent

while True:
    data_batch = sample_training_data(data, 256) # sample 256 examples
    weights_grad = evaluate_gradient(loss_func, data_batch, weights)
    weights += - step_size * weigths_grad # perform parameter update

- 전체 data set의 gradient와 loss를 계산하기 보다는, minibatch라는 작은 training sample 집합으로 나누어 학습함

- 보통 2의 승수 (32, 64, 128)

- 이 작은 minibatch를 이용해 loss의 전체 합의 '추정치'와 실제 gradient의 '추정치'를 계산