[Linear Algebra] Vectors 01

Reference : https://www.khanacademy.org/math/linear-algebra/vectors-and-spaces

 

Multiplying a vector by a scalar

a = [2 1] 라는 벡터가 있다고 하자. 원점에서 시작하면 이렇게 그려질 것.

 

 

이 벡터를 스칼라 곱을 해주게 된다면?

3a = 3[2 1] = [3*2 3*1] = [6 3]

 

 

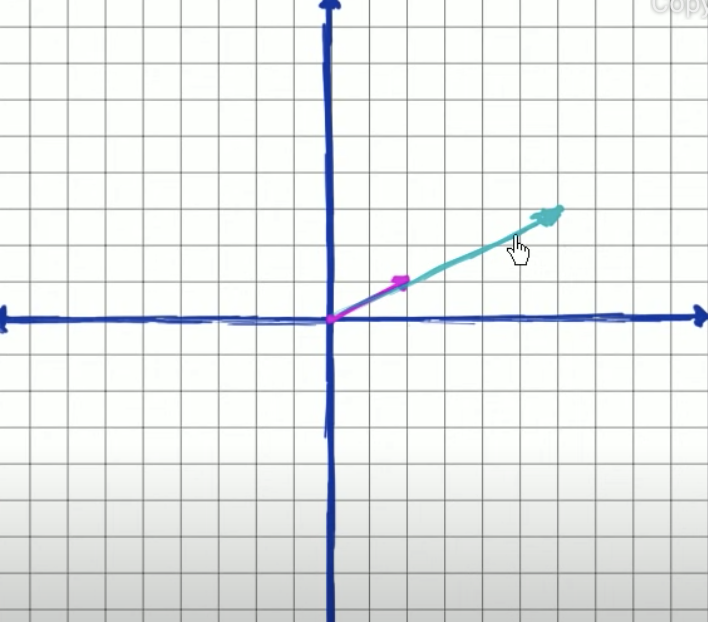
• not changed: still pointing in the same direction. 
• did change: magnitude

scalar를 곱해주면 vector을 scale up 해주구나!

 

 

---

음수(-1) 곱해줘보자.

-1a = -1[2 1] = [-2 -1]

 

 

flipped its direction!

- magnitude는 변하지 않았지만 exact opoosite direction을 가짐

 

 

---

-2a = -2[2 1] = [-4 -2]

 

 

flipped over되었고 magnitude가 2배가 되었다.

굳이 원점에서 시작할 필요는 없지만 그림에선 보기 쉽게 이렇게 그렸다.

 

 

 

---

Vector Examples

R2는 실수의 ordered 2 tuples를 의미했다. (x1, x2)

R1은 1차원이고 단순히 직선 위의 점만을 의미했다면

R2는 차원이 커져 x축, y축을 가진다.

 

 

 

a = [-1 2]

b = [3 1]

(보통 벡터는 bold체로 씀!)

 

a+b = [-1+3 2+1] = [2 3]

 

벡터는 사실 좌표상에서 어디에서든 그려도 된다.

시작점이 (x1, x2)라면 a를 표현하고 싶을 때 (x1-1, x2+2)가 된다.

ex) (-4, 4)에서 시작하면 (-4-1, 4+2) = (-5, 6)

 

 

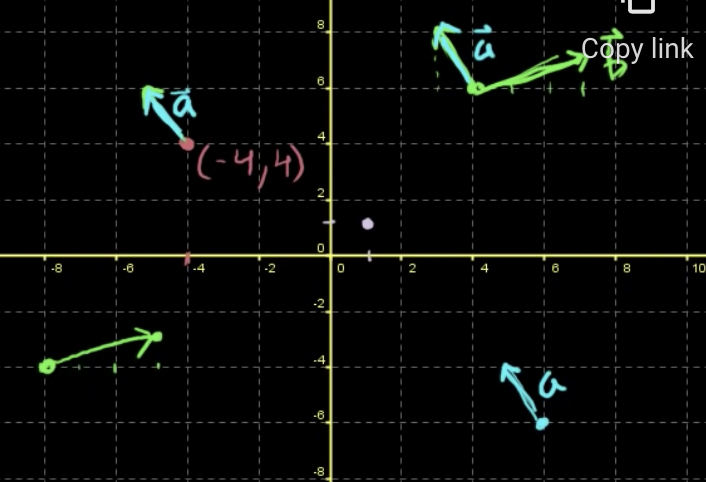
infinite numbers represent them

but, convention은 이 벡터를 origin이 initial point가 되는 standard position

 

 

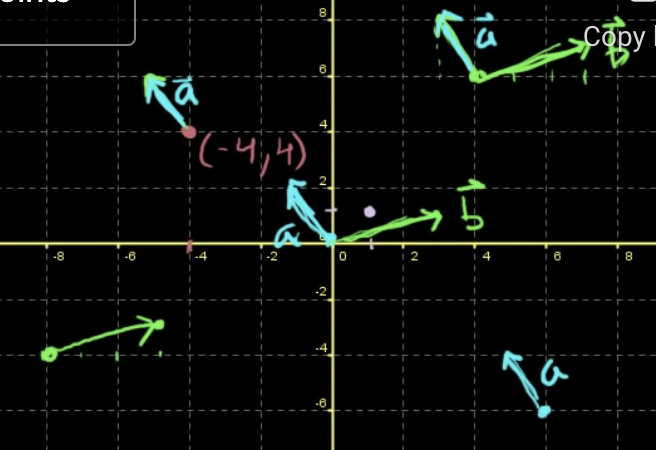
a+b도 그려본다면?

 

 

이렇게 그리면 a와 b 벡터의 관계를 잘 모를 수 있다.

but, b벡터를 a 벡터의 tail에 갖다 댄다면 잘 보일 것.

 

 

 

---

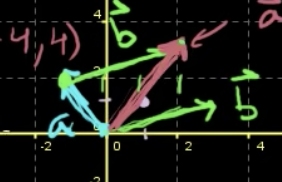
v = [1 2] 라 해보자.

2v = [2 4]

-4v = [-4 -8]

 

 

 

 

---

x = [2 4]

y = [-1 -2]

x - y = x + (-1*y) = [2 4] + [1 2] = [3 6]

 

 

 

---

x = [2 3]

y = [-4 -2]

x - y = [6 5]

 

 

 

y - x = [-6 -5]

R4에서

a = [0 -1 2 3]

b = [4 -2 0 5]

4a - 2b = 4*[0 -1 2 3] - 2*[4 -2 0 5] = [0 -4 8 12] - [8 -4 0 10] = [-8 0 8 2]